Dike and Groyne Model
From FVCOM Wiki
Introduction
It is a challenge for a terrain-following coordinate ocean model to simulate the flow field in an estuarine or coastal system with dikes and groynes. In most cases, the constructions are usually submerged during high tide but out of the water during low tide. If a vertical wall is placed within the computational domain, then terrain-following coordinate transformation can fail. Adding a slope on the surface of a dike or groyne could make the topographic coordinate transformation work, but it changes the fluid dynamics. Instead of solid blocking (no flux towards the wall) in the lower column with the dike or groyne and free exchange in the upper column above the construction, the model makes the water flow along the submerged construction under the dynamical of the sloping bottom boundary layer. As a result, this slope treatment could overestimate vertical and lateral mixing and thus produce unrealistic circulation around the construction.
Coastal inundation, which is defined as coastal flooding of normally dry land caused by heavy rains, high river discharge, tides, storm surge, tsunami processes, or some combination thereof, has been received intense attention in model applications to coastal and estuarine problems. In many coastal regions, dams are built around the area where the height of land is lower or close to the mean sea level to protect the land from flooding. An inundation forecast system is aimed at making warming of coastal flooding on an event timescale in order to facilitate evacuation and other emergency measures to protect human life and property in the coastal zone, and to accurate estimating the statistics of coastal inundation in order to enable rational planning regarding sustainable land-use practices in the coastal zone. A model used for this application must produce accurate, real-time forecasts of water level at high spatial resolution in the coastal zone and must have the capability to resolve the overtopping process of dams. These dams are like a solid wall boundary when the water level is lower than it, but become submerged constructions like dikes when flooding occurs. The wet/dry treatment technology is capable of resolving coastal flooding (Chen et al., 2006a,b), but cannot since handle a vertical seawall in the computational domain.
We have developed an unstructured grid dike and groyne treatment algorithm in a terrain-following coordinate system to calculate the velocity and tracer concentration in the coastal or estuarine system with emerged or submerged dikes and groynes. This algorithm has been coded into FVCOM with MPI parallelization, and validated for idealized cases with dike-groyne construction where analytical solutions or laboratory experiment results are available. The FVCOM with inclusion of dike and groyne treatment module has been applied to simulate the flow field off the Changjiang Estuary where a dike-groyne structure was constructed in the Deep Waterway channel in the inner shelf of the East China Sea and also to simulate the coastal inundation in Scituate Harbor, Massachusetts. The validation and application results were written up for a paper and submitted to Ocean Modeling (Ge et al. 2011). A brief description of this module is given below.
The Unstructured-Grid Dike-Groyne Algorithm
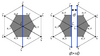
Consider a submerged dike or groyne case. For this case, the water column connected to the structure is characterized by two layers: an upper layer in which the water can flow freely across the structure, and a lower layer in which flow is blocked (with no flux into the wall). In general, the width of a dike or groyne is on the order of 2-5 m. For a numerical simulation with a horizontal resolution of > 20-100 m, these dikes or groynes can be treated as lines without width. Under this assumption, we can construct the triangular grid along dikes and groynes, with a single control volume above the structure and two separate control volumes beneath it (Fig. 7.1). The mathematic equation A detailed description of mathematics is given in Ge et al. (2011), and a brief summaryIn the Cartesian coordinate system, the vertically integrated continuity equation can be written in the form of
![\frac{\partial \zeta}{\partial t} = - \frac{1}{\Omega}\left[ \oint \left(\bar{u}D\right) \mathrm{d}y - \oint \left( \bar{v}D\right) \mathrm{d}x \right] \;\;\; Eq \; 7.1](/wiki/images/math/8/4/a/84ab3dda94a87f53b99296994530c020.png)
where ζ is the free-surface elevation, u and v are the x and y components of the horizontal velocity, D is the total water depth defined as H + , and H is the mean water depth. In FVCOM, an unstructured triangle is comprised of three nodes, a centroid, and three sides, on which u and v are placed at centroids and all scalars (i.e, ζ, H, ) are placed at nodes. u and v at centroids are calculated based on the net flux through the three sides of that triangle (shaded regions in Fig.7.1, hereafter referred to as the Momentum Control Element: MCE), while scalar variables at each node are determined by the net flux through the sections linked to centroids and the middle point of the sideline in the surrounding triangles (shaded regions in Fig.7.1), hereafter referred to as the Tracer Control Element: TCE). Ω is the area of the TCE.
Defining h as the height of dike or groyne, we divide a TCE into two element, calculate the flux individually, and then combine them. Applying (7.1) to each element, we have