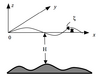
Governing Equations
From FVCOM Wiki
The governing equations consist of the following momentum, continuity, temperature, salinity, and density equations:
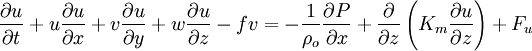
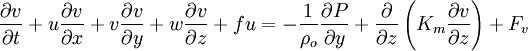
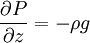
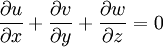
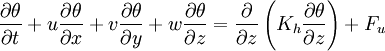

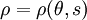

The surface and bottom boundary conditions for temperature are:
![\frac{\partial T}{\partial z} = \frac{1}{\rho c_p K_h} \left[ Q_n \left(x,y,t\right) - SW \left( x,y,\zeta,t \right) \right], \text{at} \; z = \zeta \left( x,y,t \right)](/wiki/images/math/f/4/7/f474d25e060f7c145c1fb9e8008c622d.png)
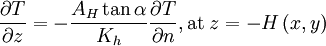
where  is the surface net heat flux, which consists of four components: downward shortwave, longwave radiation, sensible, and latent fluxes,
is the surface net heat flux, which consists of four components: downward shortwave, longwave radiation, sensible, and latent fluxes,  is the shortwave flux incident at the sea surface, and cp is the specific heat of seawater. Ah is the horizontal thermal diffusion coefficient, α is the slope of the bottom bathymetry, and n is the horizontal coordinate (Pedlosky, 1974, Chen et. al., 2004b).
is the shortwave flux incident at the sea surface, and cp is the specific heat of seawater. Ah is the horizontal thermal diffusion coefficient, α is the slope of the bottom bathymetry, and n is the horizontal coordinate (Pedlosky, 1974, Chen et. al., 2004b).
References
- Pedlosky, Joseph, 1974. Longshore currents, upwelling and bottom topography. Journal of Physical Oceanography, 4, 214–226.