Parallelization
From FVCOM Wiki
Contents |
Overview
The FVCOM code has been parallelized using a Single Processor Multiple Data (SPMD) approach [1]. The domain is decomposed using the METIS graph partitioning libraries. The interprocessor communication is explicitly defined using Message Passing Interface (MPI) calls. The resulting implementation is highly portable and will run efficiently on a variety of parallel computer architectures including both shared and distributed memory systems. The basic elements of the parallelization are as follows.
- Domain Decomposition: The domain (grid) is decomposed into N equal partitions (subdomains) where N is the number of processors to be used for the computation.
- Domain Setup: Each processor sets up an FVCOM integration in its respective subdomain.
- Data Exchange: During the calculation, information is exchanged between processors across subdomain boundaries to ensure correctness of the boundary fluxes.
- Data Collect: Output data is collected from individual processors and reconstructed into a global array before being written to disk.
Domain Decomposition
The domain decomposition is performed using the METIS graph partitioning libraries [2]. Given a list of elements, information about their connectivity and a user input desired number of partitions; METIS is tasked to assign elements to partitions under the following constraints.
- Each partition will contain roughly the same number of elements.
- The total length of the boundary between partitions is to be minimized.
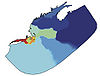
Figure 6.1 shows a 16 way partitioning of the Gulf of Maine/Georges Bank model domain. Each color represents the subdomain assigned to a given processor. Note that it is not the geographical area but rather the number of elements that is equal in each subdomain. Partitioning is performed in the horizontal only. The implicit nature of the discretization of the vertical diffusion terms in the FVCOM model make a domain decomposition in the vertical impractical. The partitioning performed by METIS occurs at the beginning of the calculation and requires a trivial amount of time to complete. Statistics on the partitions, including load balance and the number of elements assigned to each processors are written to standard output for reference.
Domain Setup
After the domain decomposition stage, each processor has been assigned a subdomain in which to integrate FVCOM. Array mappings can then be calculated to map global indices to local and vice versa. Other maps are created to coordinate data exchange across the interprocessor boundaries. Globally referenced data such as rivers, open boundary nodes, and the grid file are decomposed into the local domains using the global to local mappings. For example, if a river runs into a given processor’s subdomain, this processor will read in the river inflow data and assign it to the locally numbered node number which corresponds to the inflow river point. The other processors will ignore the data. Open boundaries and spatially varying surface forcing are treated in a similar manner. At the conclusion of this setup stage, each processor has the correct initial and boundary conditions with which to drive a full integration of its subdomain.
Data Exchange
At the boundaries between processor subdomains, data must be exchanged to preserve the correctness of the flux. The data to be exchanged is set up in a mapping procedure where interior nodes of neighboring processors along the interprocessor boundaries are mapped to the corresponding halo nodes of the exchange partner and vice-versa. For example, in Figure 6.2, computation of the flux of element E for the edge residing on the interprocessor (dark line) boundary requires information in elements H. Elements H belong to Processor 2 (P2) but they are considered halo nodes of Processor 1 (P1). Information on the current state of flow quantities in these elements must be provided by P2 in order for P1 to compute and update the fluxes of E correctly. This information is provided in an explicit interprocessor communication. Interprocessor communication of data is made using standard MPI (Message Passing Interface) non-blocking send/receive calls. The exchange subroutine is generic and can be used to exchange both element-based and node-based data for both vertically-averaged and three-dimensional flow quantities.
Performance
The efficiency of the parallel implementation can be analyzed be evaluating the performance speedup. A given model run is performed on an increasing number of processors and the time to complete the run is recorded. Speedup (S) is defined as the ratio of time to complete a job on one processor (serial) divided by the time to complete the job on N processors. Ideally, the curve should be a straight line defined by the equation S(N) = N. Various factors combine to modify code efficiency, sometimes resulting in superlinear (S(N) > N) speedup. Figure 6.3 shows the speedup measured on systems with small (< 16) number of processors. The curves do not stray far from the ideal line. The SGI Altix exhibits superlinear speedup due to its efficient network, which reduces communication overhead, and the large cache size (3 MB) of the Itanium 2 processor that boosts performance as partition size is decreased. The yellow line corresponds with a loosely coupled cluster made of the desktop computers in the MEDM lab at SMAST, which are connected by 100BaseT Ethernet. In this case the bandwidth and latency limitations of the interconnect generates significant interprocessor communication overhead resulting in a significant drop in the parallel efficiency. In the case with large number of processors (Figure 6.4): the SGI Altix maintains linear speedup up to the maximum number of tested processors (64) and the Dell 1750 series dual Pentium 4 processor nodes coupled with Myricom’s Myrinet 2000/D interconnect maintains a speedup of around 100 on 128 processors and 160 on 256, the SGI Altix remains superlinear speedup, but the computational efficiency in Dell 1750 gradually reduces as more processors are added. It should be noted that speedup is a natural measurement of parallel efficiency but not the primary metric to be evaluated when ranking computers. Job throughput and machine cost are more important criteria when selecting a machine. Excellent speedup has also been achieved on more modern systems such as IBM's Blue Gene.
Performance Model
References
- ↑ Cowles (2008). Parallelization of the FVCOM Coastal Ocean Model, International Journal of High Performance Computing Applications, 22, No. 2, 177-193.
- ↑ Karypis, G. and Kumar, V. (1998). A fast and high quality multilevel scheme for partitioning irregular graphs, SIAM Journal on Scientific Computing, 20: 359–392.