Discretization
From FVCOM Wiki
(→Discretization Stencil) |
(→Discretization Stencil) |
||
| Line 11: | Line 11: | ||
<math>[Xn(j),Yn(j)], \;\; j=1:M</math> | <math>[Xn(j),Yn(j)], \;\; j=1:M</math> | ||
| - | Since none of the triangles in the grid overlap, ''N'' should also be the total number of triangles. On each triangular cell, the three nodes are identified using integral numbers defined as <math>N_i(\hat{j})</math> where <math>\hat{j}</math> is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as <math>NBE_i(\hat{j})</math> where <math>\hat{j}</math> is counted clockwise from 1 to 3. At open or coastal solid boundaries, <math>NBE_i(\hat{j})</math> is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as ''NT(j)'', and they are counted using integral numbers ''NB<sub>i<\sub>(m) where ''m'' is counted clockwise from 1 to ''NT(j)''. | + | Since none of the triangles in the grid overlap, ''N'' should also be the total number of triangles. On each triangular cell, the three nodes are identified using integral numbers defined as <math>N_i(\hat{j})</math> where <math>\hat{j}</math> is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as <math>NBE_i(\hat{j})</math> where <math>\hat{j}</math> is counted clockwise from 1 to 3. At open or coastal solid boundaries, <math>NBE_i(\hat{j})</math> is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as ''NT(j)'', and they are counted using integral numbers ''NB<sub>i<\sub>(m)'' where ''m'' is counted clockwise from 1 to ''NT(j)''. |
Revision as of 20:23, 13 November 2011
The original version of FVCOM was developed in the σ-coordinate transformation system. The code was subsequently upgraded to the generalized terrain-following coordinate system in 2006. The discretization forms of governing equations have been significantly modified in this new coordinate system. When the non-hydrostatic version of FVCOM was developed, we implemented a semi-implicit solver, so the current version of FVCOM has two options for the time integration: 1) mode-split and 2) semi-implicit. In this chapter, we provide an example of the discrete forms of the hydrostatic FVCOM in the σ-coordinate transformation system for the mode-split solver. The σ-coordinate transformation is one selection of the generalized terrain-following coordinates, so learning the details of the discretization forms in this coordinate system can make users it easy to learn how the generalized terrain-following coordinates work in FVCOM. A brief description of the semi-implicit solver is given in Chapter 4 when the non-hydrostatic solver is introduced. Users, who are interested in learning the details of discretization forms in the generalized terrain-following coordinate system, can examine the source code directly.
Discretization Stencil
Similar to a triangular finite element method, the horizontal numerical computational domain is subdivided into a set of non-overlapping unstructured triangular cells. An unstructured triangle is comprised of three nodes, a centroid, and three sides (Fig. 3.1). Let N and M be the total number of centroids and nodes in the computational domain, respectively, then the locations of centroids can be expressed as:
![[X(i),Y(i)], \; \; i=1:N](/wiki/images/math/2/e/5/2e5b85ad9c13cc99f44e7236d8c7aa7e.png)
and the location of the nodes can be specified as:
![[Xn(j),Yn(j)], \;\; j=1:M](/wiki/images/math/7/6/6/76670507d693e461bbfdab330eddf6f6.png)
Since none of the triangles in the grid overlap, N should also be the total number of triangles. On each triangular cell, the three nodes are identified using integral numbers defined as 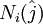 where
where 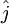 is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as
is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as 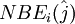 where
where 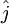 is counted clockwise from 1 to 3. At open or coastal solid boundaries,
is counted clockwise from 1 to 3. At open or coastal solid boundaries, 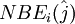 is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as NT(j), and they are counted using integral numbers NBi<\sub>(m) where m is counted clockwise from 1 to NT(j).
is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as NT(j), and they are counted using integral numbers NBi<\sub>(m) where m is counted clockwise from 1 to NT(j).