Discretization
From FVCOM Wiki
The original version of FVCOM was developed in the σ-coordinate transformation system. The code was subsequently upgraded to the generalized terrain-following coordinate system in 2006. The discretization forms of governing equations have been significantly modified in this new coordinate system. When the non-hydrostatic version of FVCOM was developed, we implemented a semi-implicit solver, so the current version of FVCOM has two options for the time integration: 1) mode-split and 2) semi-implicit. In this chapter, we provide an example of the discrete forms of the hydrostatic FVCOM in the σ-coordinate transformation system for the mode-split solver. The σ-coordinate transformation is one selection of the generalized terrain-following coordinates, so learning the details of the discretization forms in this coordinate system can make users it easy to learn how the generalized terrain-following coordinates work in FVCOM. A brief description of the semi-implicit solver is given in Chapter 4 when the non-hydrostatic solver is introduced. Users, who are interested in learning the details of discretization forms in the generalized terrain-following coordinate system, can examine the source code directly.
Computational Stencil
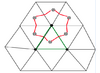
Similar to a triangular finite element method, the horizontal numerical computational domain is subdivided into a set of non-overlapping unstructured triangular cells. An unstructured triangle is comprised of three nodes, a centroid, and three sides (Fig. 3.1). Let N and M be the total number of centroids and nodes in the computational domain, respectively, then the locations of centroids can be expressed as:
![[X(i),Y(i)], \; \; i=1:N](/wiki/images/math/2/e/5/2e5b85ad9c13cc99f44e7236d8c7aa7e.png)
and the location of the nodes can be specified as:
![[Xn(j),Yn(j)], \;\; j=1:M](/wiki/images/math/7/6/6/76670507d693e461bbfdab330eddf6f6.png)
Since none of the triangles in the grid overlap, N should also be the total number of triangles. On each triangular cell, the three nodes are identified using integral numbers defined as 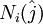 where
where 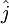 is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as
is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as 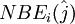 where
where 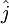 is counted clockwise from 1 to 3. At open or coastal solid boundaries,
is counted clockwise from 1 to 3. At open or coastal solid boundaries, 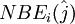 is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as NT(j), and they are counted using integral numbers NBi(m) where m is counted clockwise from 1 to NT(j).
is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as NT(j), and they are counted using integral numbers NBi(m) where m is counted clockwise from 1 to NT(j).
To provide a more accurate estimation of the sea-surface elevation, currents and salt and temperature fluxes, u and v are placed at centroids and all scalar variables, such as ζ, H, , ω, S, T, ρ, are placed at nodes. Scalar variables at each node are determined by a net flux through the sections linked to centroids and the mid-point of the adjacent sides in the surrounding triangles (called the “tracer control element” or TCE), while u and v at the centroids are calculated based on a net flux through the three sides of that triangle (called the “momentum control element” or MCE). Similar to other finite-difference models such as POM and ROMS, all the model variables except ω (vertical velocity on the sigma-layer surface) and turbulence variables (such as and ) are placed at the mid-level of each σ layer. There are no restrictions on the thickness of the σ-layer, which allows users to use either uniform or non-uniform σ-layers.
Discretization in Cartesian Coordinates
2D External Mode
Let us consider the continuity equation first. Integrating Eq. (2.30) over a given triangle area yields:
![\iint \limits_{\Omega} \frac{\partial \zeta}{\partial t} \mathrm{d}x\mathrm{d}y = - \iint \limits_{\Omega}\left[\frac{\partial(\bar{u}D)}{\partial x} + \frac{\partial(\bar{v}D)}{\partial y} \right] \mathrm{d}x\mathrm{d}y = - \oint \limits_{s'} \bar{v}_n D \mathrm{d}s'](/wiki/images/math/e/d/e/edeabaf15db6bcb837c363d99eeb8bc0.png)
where 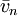 is the velocity component normal to the sides of the triangle and s' is the closed trajectory comprised of the three sides. This equation is integrated numerically using a modified fourth-order Runge-Kutta time-stepping scheme. This is a multi-stage time-stepping approach with second-order temporal accuracy. The detailed procedure for this method is described as follows:
is the velocity component normal to the sides of the triangle and s' is the closed trajectory comprised of the three sides. This equation is integrated numerically using a modified fourth-order Runge-Kutta time-stepping scheme. This is a multi-stage time-stepping approach with second-order temporal accuracy. The detailed procedure for this method is described as follows: