Discretization
From FVCOM Wiki
| Line 19: | Line 19: | ||
==Discretization in Cartesian Coordinates== | ==Discretization in Cartesian Coordinates== | ||
| + | |||
| + | <amsmath> | ||
| + | \label{e:barwq}\begin{split} | ||
| + | H_c&=\frac{1}{2n} \sum^n_{l=0}(-1)^{l}(n-{l})^{p-2} | ||
| + | \sum_{l _1+\dots+ l _p=l}\prod^p_{i=1} \binom{n_i}{l _i}\\ | ||
| + | &\quad\cdot[(n-l )-(n_i-l _i)]^{n_i-l _i}\\ | ||
| + | &\quad\cdot | ||
| + | \Bigl[(n-l )^2-\sum^p_{j=1}(n_i-l _i)^2\Bigr]. | ||
| + | \end{split} | ||
| + | </amsmath> | ||
===2D External Mode=== | ===2D External Mode=== | ||
Revision as of 14:40, 14 November 2011
The original version of FVCOM was developed in the σ-coordinate transformation system. The code was subsequently upgraded to the generalized terrain-following coordinate system in 2006. The discretization forms of governing equations have been significantly modified in this new coordinate system. When the non-hydrostatic version of FVCOM was developed, we implemented a semi-implicit solver, so the current version of FVCOM has two options for the time integration: 1) mode-split and 2) semi-implicit. In this chapter, we provide an example of the discrete forms of the hydrostatic FVCOM in the σ-coordinate transformation system for the mode-split solver. The σ-coordinate transformation is one selection of the generalized terrain-following coordinates, so learning the details of the discretization forms in this coordinate system can make users it easy to learn how the generalized terrain-following coordinates work in FVCOM. A brief description of the semi-implicit solver is given in Chapter 4 when the non-hydrostatic solver is introduced. Users, who are interested in learning the details of discretization forms in the generalized terrain-following coordinate system, can examine the source code directly.
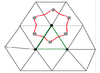
Computational Stencil
Similar to a triangular finite element method, the horizontal numerical computational domain is subdivided into a set of non-overlapping unstructured triangular cells. An unstructured triangle is comprised of three nodes, a centroid, and three sides (Fig. 3.1). Let N and M be the total number of centroids and nodes in the computational domain, respectively, then the locations of centroids can be expressed as:
![[X(i),Y(i)], \; \; i=1:N](/wiki/images/math/2/e/5/2e5b85ad9c13cc99f44e7236d8c7aa7e.png)
and the location of the nodes can be specified as:
![[Xn(j),Yn(j)], \;\; j=1:M](/wiki/images/math/7/6/6/76670507d693e461bbfdab330eddf6f6.png)
Since none of the triangles in the grid overlap, N should also be the total number of triangles. On each triangular cell, the three nodes are identified using integral numbers defined as 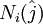 where
where 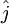 is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as
is counted clockwise from 1 to 3. The surrounding triangles that have a common side are counted using integral numbers defined as 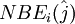 where
where 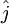 is counted clockwise from 1 to 3. At open or coastal solid boundaries,
is counted clockwise from 1 to 3. At open or coastal solid boundaries, 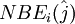 is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as NT(j), and they are counted using integral numbers NBi(m) where m is counted clockwise from 1 to NT(j).
is specified as zero. At each node, the total number of the surrounding triangles with a connection to this node is expressed as NT(j), and they are counted using integral numbers NBi(m) where m is counted clockwise from 1 to NT(j).
To provide a more accurate estimation of the sea-surface elevation, currents and salt and temperature fluxes, u and v are placed at centroids and all scalar variables, such as ζ, H, , ω, S, T, ρ, are placed at nodes. Scalar variables at each node are determined by a net flux through the sections linked to centroids and the mid-point of the adjacent sides in the surrounding triangles (called the “tracer control element” or TCE), while u and v at the centroids are calculated based on a net flux through the three sides of that triangle (called the “momentum control element” or MCE). Similar to other finite-difference models such as POM and ROMS, all the model variables except ω (vertical velocity on the sigma-layer surface) and turbulence variables (such as and ) are placed at the mid-level of each σ layer. There are no restrictions on the thickness of the σ-layer, which allows users to use either uniform or non-uniform σ-layers.
Discretization in Cartesian Coordinates
<amsmath> \label{e:barwq}\begin{split} H_c&=\frac{1}{2n} \sum^n_{l=0}(-1)^{l}(n-{l})^{p-2} \sum_{l _1+\dots+ l _p=l}\prod^p_{i=1} \binom{n_i}{l _i}\\ &\quad\cdot[(n-l )-(n_i-l _i)]^{n_i-l _i}\\ &\quad\cdot \Bigl[(n-l )^2-\sum^p_{j=1}(n_i-l _i)^2\Bigr]. \end{split} </amsmath>
2D External Mode
</math>